WorkFlowyのトピック階層構造の説明
公開日:
:
WorkFlowy
1.WorkFlowyの特徴は、トピックの階層構造
(1) WorkFlowyは、トピックを階層構造で管理するテキスト管理システム
WorkFlowyは、テキストを管理するシステムです。WorkFlowyは、「トピック階層構造で管理する」ことによって、テキストを管理します。
WorkFlowyがテキストを管理する枠組みは、「テキストをトピックに格納する」と「トピックを階層構造で管理する」の2段階
WorkFlowyは、Zoom機能や折りたたみ機能、トピック移動機能など、いくつかの便利な機能を持っています。これらの機能がうまく機能するのは、WorkFlowyがトピックを階層構造で管理しているためです。トピックへのZoomも、トピックの折りたたみも、トピックの移動も、トピック階層構造を前提としています。
この意味で、トピックを階層構造で管理することは、WorkFlowyのテキスト管理システムの中核です。
そのため、WorkFlowyのトピック階層構造それ自体を理解することは、WorkFlowyそのものに対する理解を深めることになり、ひいては、WorkFlowyというテキスト管理システムをうまく機能させることにつながります。
(2) WorkFlowyのトピック階層構造は、WorkFlowy唯一の秩序
ところで、WorkFlowyのトピック階層構造は、WorkFlowyが持つ唯一の秩序です。
多くのデジタルツールは、同時にいろんな秩序を持ち、ユーザーの要望に合わせて、いろんな秩序でデータを表示します。でも、WorkFlowyは、同時にはひとつの秩序でしかデータを表示することができません。
WorkFlowyに存在する秩序は、順番と深さからなる二次元の階層構造ただひとつ(「ただひとつ」というWorkFlowyの思想その3)
たとえばEvernoteは、以下のことが可能です。
- 特定のノートブックに属するノートを、更新日順に並べて表示する
- 特定のタグがついたノートを、名前順に並べて表示する
- すべてのノートの中から、「Evernote」という単語を含むノートを抜き出して表示する
また、ToodledoやTodoistなら、以下のことが可能です。
- 特定のプロジェクトに属するタスクを、締め切り順に並べて表示する
- 今日が締切のタスクだけを抜き出して表示する
- 所要見込み時間が30分以下のタスクを、重要度が高い順に並べて表示する。
なぜEvernoteやToodledoにこんなことができるかといえば、EvernoteやToodledoが、データが持つ情報を使って、データを抽出したり並べ替えたりする機能を持っているからです。この意味で、EvernoteやToodledoは、データベースです。
これに対して、WorkFlowyは、データが持つ情報を使って、データを抽出したり、並べ替えたり、といった機能を、ほとんど用意していません。WorkFlowyには並べ替え機能がありませんし、また、WorkFlowyの検索機能はデータを抽出する機能ではなく、トピックを折りたたむ機能だからです。この意味で、WorkFlowyはデータベースではなく、リストです。
データベースとリスト(ひとつの秩序でいろんな役割を果たすための、WorkFlowyの発想)
このように、WorkFlowyは、ただひとつの秩序しか持ちません。WorkFlowyのトピック階層構造は、WorkFlowyが持つ、唯一の秩序です。
2.WorkFlowyのトピック階層構造の考察
WorkFlowyのトピック階層構造は、「順番」と「深さ」という2つの座標軸で構成される二次元です。
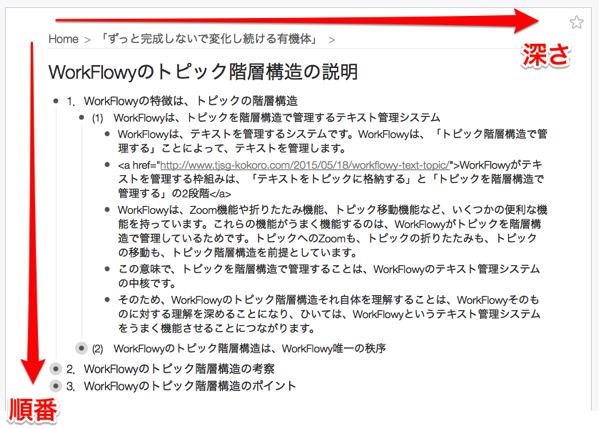
基本的には、これだけです。
しかし、細かく見ていくと、この二次元の階層構造には、いくつかの特徴があります。
以下、この特徴をひとつひとつ見ていきます。
(1) 左上に原点があり、すべてのトピックが原点からつながっている
まず、WorkFlowyの階層構造は、左上に原点があり、すべてのトピックが原点からつながっています。
a.左上に原点がある
2つの座標軸で構成される二次元には、2つの座標軸が交わる原点があります。
多くの二次元は、真ん中に原点を持っています。
たとえば、中学数学とかでよく出てくるXY座標は、こんな感じです。
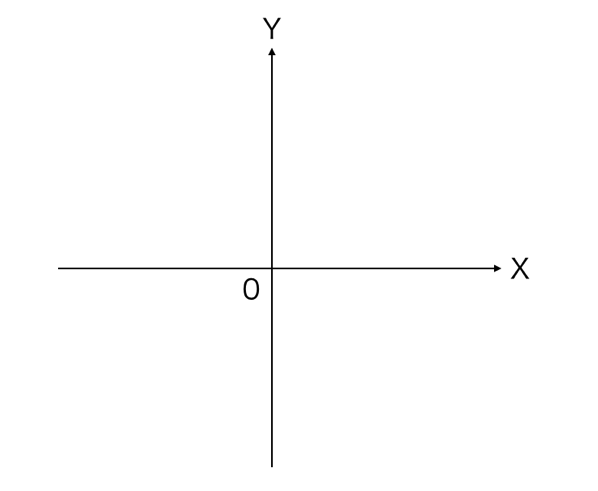
真ん中に原点があって、X軸もY軸も、原点から両方向に広がっています。
これに対して、WorkFlowyの原点は、左上です。「順番」の次元は原点から下にのみ広がり、「深さ」の次元は原点から右にのみ広がります。

b.すべてのトピックが原点からつながっている
次に、WorkFlowyの階層構造は、すべてのトピックが、原点からつながっています。
(a) 「順番」の座標軸におけるつながり
まず、「順番」の座標軸については、トピックとトピックとの間に、トピック以外の何か、たとえば空白行や区切り線を入れることができません。
テキストを格納していない空白トピックを作ることならできます。
でも、トピック自体が存在しない空白行や、トピックではない区切り線などを、トピックとトピックの間に入れることはできません。
(b) 「深さ」の座標軸におけるつながり
次に、「深さ」の座標軸については、階層のレベルを飛ばすことができません。
WorkFlowyでは、あるトピックの子トピックの階層レベルは、必ず、親トピックの階層レベルよりも1つ深い階層レベルになります。

これを他のツールと比較してみます。
たとえばWordは、このような階層レベルを飛ばした親子関係を持つ階層を作ることができます。

また、Evernoteのリスト機能でも、階層レベルを飛ばした親子関係を持つ階層を作ることができます。
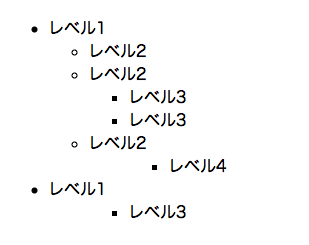
しかし、WorkFlowyでは、できません。WorkFlowyの階層構造では、親トピックよりも2つ以上深い階層レベルの子トピックを作ることができません。
c.左上への重力
「左上に原点があり、すべてのトピックが原点からつながっている」との特徴は、「左上への重力がある」というイメージで把握できます。
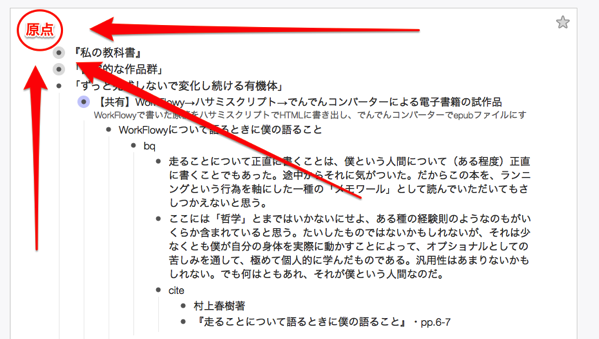
「順番」の座標軸では、上に向けての重力があります。
上に向けての重力があるので、ある順番にトピックを作るには、その順番よりもひとつ上の順番に、トピックが存在していなければいけません。

「深さ」の座標軸では、左に向けての重力があります。
左に向けての重力があるので、あるトピックの深さは、そのトピックのひとつ上の順番のトピックの階層レベルよりも、ひとつだけ深い階層レベルまでしか選べません。

これに対して、紙に書くメモや、マンダラートや、マインドマップには、左上への重力がありません。
左上への重力は、WorkFlowyの階層構造を特徴づけるひとつめのポイントです。
(2) 「順番」と「深さ」という2つの座標軸に、自然数の目盛りが付いている
次に、WorkFlowyの階層構造を構成する「順番」と「深さ」という2つの座標軸には、自然数の目盛りがついています。
a.トピックの数と階層レベルの数
WorkFlowyの二次元は、自然数の目盛りのついた二次元です。
なぜなら、「順番」の次元はトピックの数、「深さ」の次元は階層のレベルなので、いずれも数えられるものだからです。WorkFlowyにおいては、「順番」の座標軸も「深さ」の座標軸も、1の次は2で、4の次は5、101の次は102です。

b.連続量でなく、離散量
別の観点から言うと、WorkFlowyが用意する目盛りは、アナログ量ではなく、デジタル量です。
アナログ量とは、連続量ともいい、連続している数量です。これに対して、デジタル量は、離散量ともいい、連続していない数量です。
- デジタル量=離散量
- アナログ量=連続量
WorkFlowyは、ひとつめのトピックとふたつめのトピックの間は途切れています。なので、WorkFlowyの二次元を構成する「順番」と「深さ」は、いずれも離散量です。
c.自然数の目盛り
まとめると、WorkFlowyの二次元を構成する「順番」と「深さ」という座標軸には、自然数の目盛りがついています。WorkFlowyのトピックは、(原点からつながってはいるけれど、)途切れなくつながっているのではなく、離散量として並んでいます。
これに対して、同じ二次元である紙のメモやマインドマップには自然数の目盛りがついていません。紙のメモやマインドマップは、複数の事項を途切れなくつなぐことができます。
自然数の目盛りにより、トピックが離散量として存在すること。これが、WorkFlowyのトピック階層構造を特徴づけるふたつめのポイントです。
(3) すべての階層が、1:1以上(原点から広がり続ける)
さらに、WorkFlowyの階層構造は、すべての階層の親子関係が、1:1以上の関係です。そのため、原点から広がり続ける構造をしています。
a.すべての階層の親子関係が、1:1以上
WorkFlowyの階層構造は、階層ごとに、親子関係を持っています。
この親子関係は、すべての階層において、1:1以上の関係になっています。
親:子=1:1以上
です。
ポイントは、親の数が1であることです。子の数に制限はありません(1以上)が、親の数は必ず1です。

この点で、WorkFlowyの階層構造は、(両性を有する)生物の家系図とは大きく異なります。生物の家系図は、父と母から子が生まれますので、親子関係が2:1以上だからです。
b.親から子を見ると
この階層構造を、親トピックの側から見れば、
- 自分の子トピックの親トピックは、自分だけ。自分の子トピックに、自分以外の親トピックが存在することはありえない。
- 自分の孫トピックの祖父母トピックは、自分だけ。自分の孫トピックに、自分以外の祖父母トピックが存在することはありえない。
- 自分の子孫トピックの先祖は、自分世代では、自分だけ。
となります。

自分の子トピック、孫トピック、もっと先の子孫トピックは、自分や自分の先祖・子孫だけの子孫です。自分や自分の先祖・子孫系列以外に、自分の子孫トピックの先祖トピックは存在しません。
c.子から親を見る
また、この階層構造を、子トピックの側から見れば、
- 自分の直近の親トピックは、ただひとつだけ
- 自分の親トピックの親トピックも、ただひとつだけ
- 自分の先祖トピックは、世代ごとに、ただひとつずつ
となります。
つまり、WorkFlowyに存在するトピックのすべてについて、
- そのトピックの親トピックはどのトピックか?
- そのトピックの親トピックの親トピックはどのトピックか?
- そのトピックのX世代上の先祖トピックはどのトピックか?
が、すべてひとつのトピックに特定できる、ということです。
d.原点から広がり続ける階層構造
WorkFlowyの階層構造は、すべての親子関係が1:1以上です。ということは、先祖までさかのぼり続ければ、すべてのトピックはひとつの先祖にたどり着きます。
このすべての先祖トピックが、Homeです。このHomeは、「順番」と「深さ」という2つの座標軸が0,0で交わる原点でもあります。

WorkFlowyの階層構造は、Homeという原点から広がり続ける階層構造です。
3.WorkFlowyのトピック階層構造のポイント
まとめます。
まず、WorkFlowyのトピックは、階層構造を持っています。この階層構造は、WorkFlowyが持つ唯一の秩序です。
次に、WorkFlowyの階層構造は、「順番」と「深さ」という2つの座標軸で構成される二次元です。この二次元の階層構造には、次の3つの特徴があります。
- (1) 左上に原点があって、すべてのトピックが原点からつながっている。
- (2) 「順番」の座標軸にも、「深さ」の座標軸にも、自然数の目盛りがついている。
- (3) すべての階層における親子関係が1:1以上で、原点から広がり続ける構造になっている。
つまり、WorkFlowyのトピック階層構造は、Homeという原点から「順番」と「深さ」という2つの方向に、離散量で広がっています。
WorkFlowyのなかに存在するすべてのトピックは、元をたどれば、Homeというただひとつの原点から生まれています。これが、WorkFlowyのトピック階層構造です。
スポンサードリンク
関連記事
-

-
WorkFlowyは、文書作成に、どんな革命をもたらすか?
1.はじめに(Amazonの「文書作成ソフト」ランキング) 2016年1月29日、『クラウド時代の思
-

-
WorkFlowyのZoom機能の細かいルール(1)
Zoom機能は、WorkFlowyの中核的機能です。 WorkFlowyの中核機能「Zoom」の説明
-

-
【連載】WorkFlowyのテキスト入力に関するキー操作の基本(1) Enterキーの挙動
WorkFlowyは、テキストを階層構造で管理するシステムです。テキストをトピックに格納し、トピック
-

-
WorkFlowyの公式デモページで、アカウントを作成せずに、WorkFlowyを体験する
WorkFlowyは、ある種の人にとっては、うまく機能し、大きな力を発揮します。 自分にとってWor
-

-
WorkFlowyのImportの基本(テキストファイル、Excel、Evernote)
1.WorkFlowyのImportとExportは、WorkFlowyと他のツールをつなぐ Wor
-

-
なぜ、MemoFlowyを使うのか?(3) 書いたメモを、WorkFlowyのアウトラインの中の好きな場所へ簡単に放り込める
MemoFlowyは、WorkFlowyにテキストメモを投稿するためのiOS用アプリです。ぱっとアプ
-

-
WorkFlowyをプレゼン資料として使ってみたことの報告(後編:新たな試行錯誤とそこから得た収穫)
1.はじめに ここしばらくの間、私は、WorkFlowyをプレゼン資料として使うことに取り組んでいま
-

-
『WorkFlowy文章作法』の「はじめに」
本書について こんにちは。本書『WorkFlowy文章作法』では、 WorkFlowyで文章を書く
-

-
「WorkFlowy専用Firefox」の余白を、アドオン「Stylish」で調整する
1.「WorkFlowy専用Firefox」で、これができればいいなと思っていたこと (1) 「Wo
-

-
現にうまく機能しているWorkFlowyを使った文章の書き方
私にとって、WorkFlowyは、文章を書くための道具です。 WorkFlowyで文章を書くことのメ

